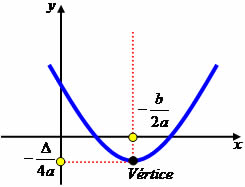
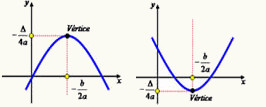
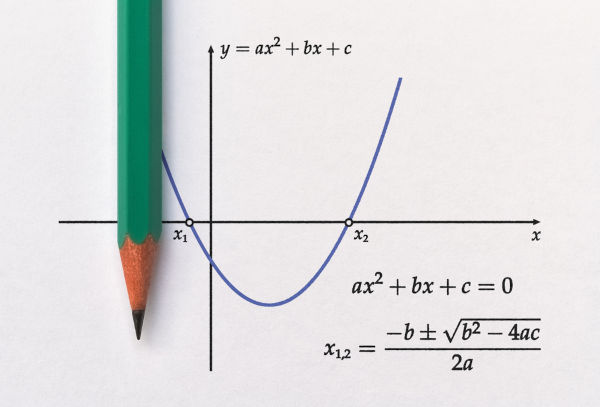
O gráfico de uma função do 2º grau é dado por uma parábola com concavidade voltada para cima ou para baixo. A parábola intersecciona ou não, o eixo das abscissas (x), isso depende do tipo de equação do 2º grau que compõe a função. Para obtermos a condição dessa parábola em relação ao eixo x, precisamos aplicar o método de Bháskara, trocando f(x) ou y por zero. Devemos sempre lembrar que uma equação do 2º grau é dada pela expressão ax² + bx + c = 0, onde os coeficientes a, b e c são números reais e a deve ser diferente de zero. Uma função do 2º grau respeita a expressão f(x) = ax² + bx + c ou y = ax² + bx + c, onde x e y são pares ordenados pertencentes ao plano cartesiano e responsáveis pela construção da parábola.
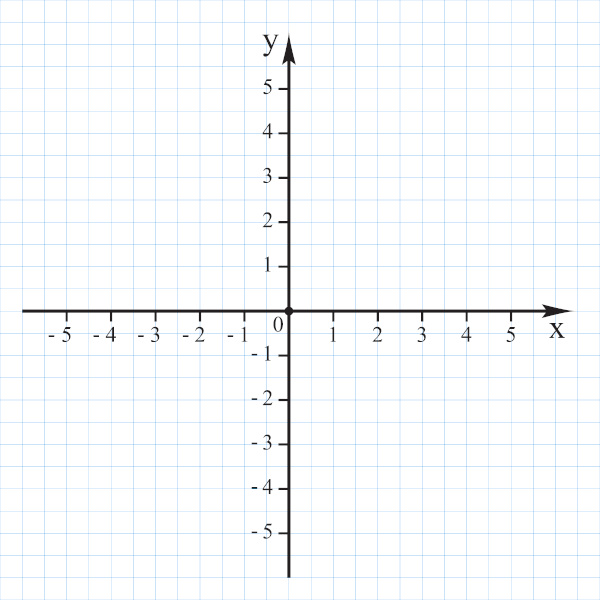
O plano cartesiano responsável pela construção das funções é dado pela intersecção de dois eixos perpendiculares, enumerados de acordo com a reta numérica dos números reais. Todo número do eixo x possui imagem correspondente no eixo y, de acordo com a função fornecida. Observe uma representação do plano cartesiano:
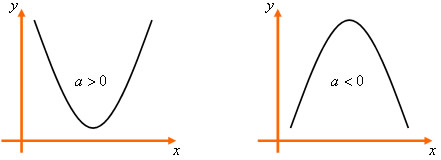
Vamos demonstrar as posições de uma parábola de acordo com o número de raízes e o valor do coeficiente a, que ordena a concavidade voltada para cima ou para baixo.
Condições
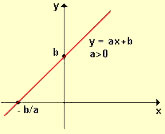
a > 0, parábola com a concavidade voltada para cima.
a < 0, parábola com a concavidade voltada para baixo.
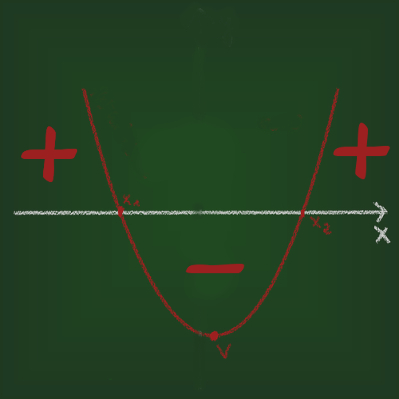
? > 0, a parábola intercepta o eixo das abscissas em dois pontos.
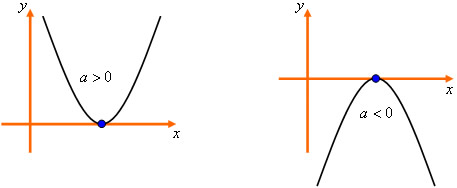
? = 0, a parábola intercepta o eixo das abscissas somente em um ponto.
? < 0, a parábola não intercepta o eixo das abscissas.
? > 0
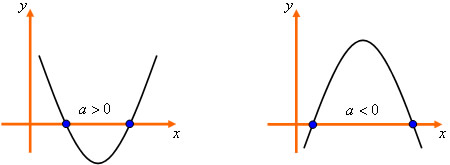
? = 0
? < 0
Observe algumas funções do 2º grau e seus respectivos gráficos.
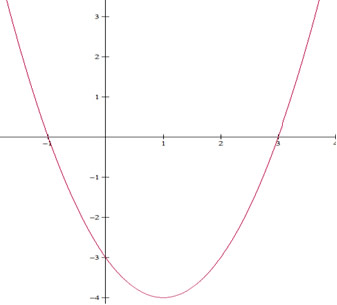
Exemplo 1
f(x) = x² – 2x – 3
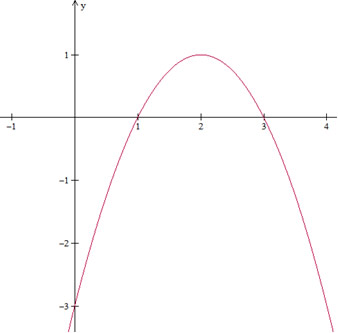
Exemplo 2
f(x) = –x² + 4x – 3
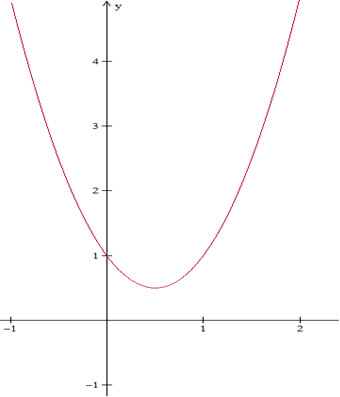
Exemplo 3
f(x) = 2x² – 2x + 1
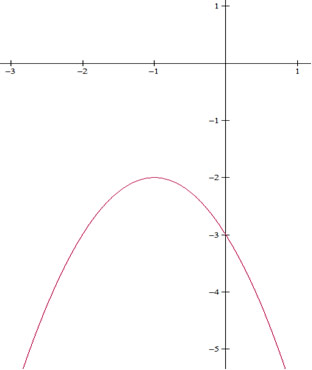
Exemplo 4
f(x) = –x² – 2x – 3
Aproveite para conferir nossa videoaula sobre o assunto: