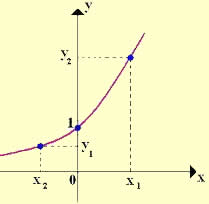
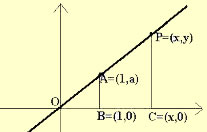
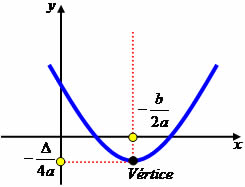
Toda expressão na forma y = ax + b ou f(x) = ax + b, onde a e b são números reais e a ≠ 0, é considerada uma função do 1º grau. Exemplos:
y = 2x + 9, a = 2 e b = 9
y = –x – 1, a = – 1 e b = – 1
y = 9x – 5, a = 9 e b = – 5
y = (1/3)x + 7, a = 1/3 e b = 7
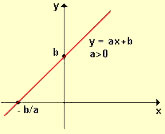
Uma função do 1º grau possui representação no plano cartesiano através de uma reta, podendo a função ser crescente ou decrescente, o que determinará a posição da reta.
Função crescente (a > 0)
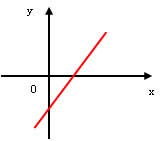
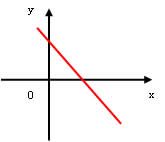
Função decrescente (a < 0)
Função constante

Para determinarmos o zero ou a raiz de uma função basta considerarmos f(x) = 0 ou y = 0.
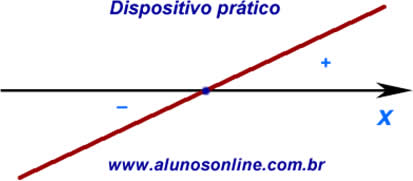
Raiz ou zero da função é o instante em que a reta corta o eixo x.
f(x) = ax + b
f(x) = 0
ax + b = 0
ax = – b
x = – (b/a)
Exemplo 1
Obtendo a raiz da função f(x) = 3x – 6
3x – 6 = 0
3x = 6
x = 6/3
x = 2
A raiz da função é igual a 2.
Exemplo 2
Seja f uma função real definida pela lei de formação f(x) = 2x + 1. Qual é a raiz dessa função?
F(x) = 0
2x + 1 = 0
2x = –1
x = – 1/2
Aproveite para conferir nossas videoaulas relacionadas ao assunto: