Função é o nome dado a uma regra que relaciona elementos a partir dos padrões matemáticos criados para elas. O modo como os elementos desses conjuntos relacionam-se pode classificar uma função como injetora e/ou sobrejetora. As funções que são injetoras e sobrejetoras ao mesmo tempo são chamadas de bijeções, ou funções bijetivas, ou funções bijetoras.
Fica claro, portanto, que é necessário conhecer pelos menos a definição de função, de função injetora e função sobrejetora para compreender bem o que são bijeções. Por isso, antes de explicar as funções bijetoras com mais detalhes, discutiremos rapidamente esses três conceitos.
Definição de função
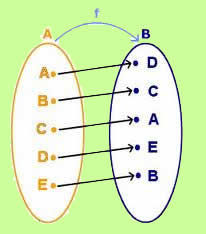
Considere dois conjuntos A e B, uma função é uma regra que relaciona cada elemento do conjunto A a um único elemento do conjunto B. Quando envolvem conjuntos numéricos, as funções são fórmulas que ligam cada número de um conjunto com um único número de um segundo conjunto.
Ainda nessa definição, o conjunto A representa uma variável independente e é chamado de domínio. O conjunto B representa uma variável dependente (dos elementos de A) e é chamado de contradomínio. Todo elemento x pertencente a A possui pelo menos um representante y pertencente ao conjunto B. O conjunto formado por todo os elementos y de B, que são imagens dos elementos x de A, é subconjunto de B e é chamado de imagem.
Antes de partirmos para os exemplos, observe apenas que, em se tratando de conjuntos numéricos, é comum que os conjuntos A e B sejam iguais ou que um seja subconjunto do outro.
Exemplo:
y = 2x, com x pertencente aos números naturais, é a função que “liga” o conjunto dos números naturais ao conjunto dos números pares, que é subconjunto do domínio. Nesse exemplo, o domínio é formado por todos os números inteiros positivos, bem como o contradomínio, e a imagem é formada pelo conjunto dos números pares.
Funções injetoras
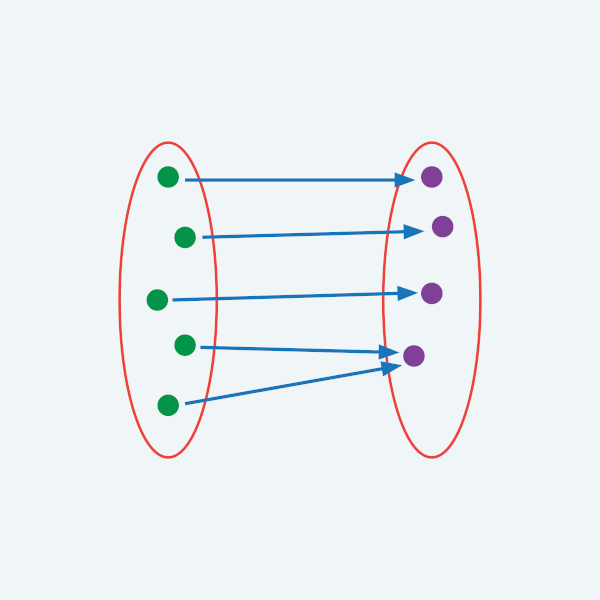
A definição de função garante que um elemento de A possui um único representante em B, mas alguns elementos de B podem ser resultados de mais de um elemento de A. Esse é o caso da função y = x2, em que os elementos 2 e – 2, pertencentes a A, estão ligados ao elemento 4, pertencente a B.
Em uma função injetora, isso não acontece, pois elementos distintos de A estão ligados a elementos distintos de B e não existem dois ou mais elementos de A ligados ao mesmo elemento de B.
Funções sobrejetoras
Uma função é chamada de sobrejetora quando o seu contradomínio é igual à imagem. Qualquer função pode tornar-se sobrejetora, bastando para isso redefini-la, tomando sua imagem como contradomínio.
Funções bijetoras
As funções bijetoras, como dito, são injetoras e sobrejetoras ao mesmo tempo. Uma função bijetora possui as seguintes características:
-
O contradomínio é igual à imagem;
-
Se existe y pertencente a B, então, existe x pertencente a A (y = f(x));
-
Um elemento do domínio está ligado a um único elemento da imagem e um elemento da imagem está ligado a um único elemento do domínio.
Nas funções bijetoras, todos os elementos do contradomínio são imagens de algum elemento do domínio.
Exemplos:
y = 2x, com domínio nos números naturais e contradomínio nos números pares.
y = x2, com domínio e contradomínio nos números reais positivos.
Aproveite para conferir nossa videoaula relacionada ao assunto: