Função polinomial

 Definimos como função polinomial uma função em que a lei de formação é um polinômio. Existem diferentes tipos de funções polinomiais, que são nomeadas de acordo com o grau do polinômio que descreve a sua lei de formação, como a função polinomial do 1º grau, a função polinomial do 2º grau e assim sucessivamente. Para calcular o valor numérico de uma função polinomial, basta substituir o valor dado em sua lei de formação e calcular o valor numérico da expressão algébrica.

Ao realizar o estudo de funções polinomiais, é bastante recorrente a representação gráfica da função. Quando representamos uma função polinomial do 1º grau no plano cartesiano, o seu gráfico é sempre uma reta. Já a função polinomial do 2º grau possui o gráfico no formato de uma parábola. É possível também fazer a representação gráfica de funções polinomiais com graus maiores, se necessário.

Leia também: Diferenças entre função e equação

Tópicos deste artigo

• 1 - Resumo
• 2 - O que é uma função polinomial?
• 3 - Grau de uma função polinomial
  • Função polinomial do 1º grau ou função afim
  • Função polinomial do 2º grau ou função quadrática
  • Função polinomial do 3º grau ou função cúbica
  • Função polinomial do 4º grau
  • Função polinomial do 5º grau
  • Função polinomial do 6º grau
• 4 - Valor numérico da função
• 5 - Gráfico da função polinomial
  • Gráfico de uma função polinomial do 1º grau
  • Gráfico de uma função polinomial do 2º grau
  • Gráfico de uma função do 3º grau
• 6 - Igualdade de polinômios
• 7 - Operações com polinômios
  • Adição de polinômios
  • Subtração de polinômios
  • Multiplicação de polinômios
  • Divisão de polinômios
• 8 - Exercícios resolvidos sobre função polinomial

Resumo

• Função polinomiais são funções cuja lei de formação é um polinômio.

• De modo geral, a lei de formação da função polinomial de grau n é:

f(x) = a_n . xⁿ + a_{n – 1} . x^{n – 1} + ...+a₂ . x² + a₁ . x + a₀

• As funções polinomiais recebem nomes de acordo com o grau do polinômio.

• Para calcular o valor numérico da função, basta substituir a variável pelo valor desejado.

• O gráfico de uma função polinomial do 1º grau é sempre uma reta.

• O gráfico de uma função polinomial do 2º grau é sempre uma parábola.

• O gráfico de uma função polinomial do 3º grau é sempre uma cúbica.

O que é uma função polinomial?

Conhecemos como função polinomial qualquer função f: A → B em que a lei de formação é um polinômio de grau n.

• x é a variável.

• n é um número natural.

• a_n, a_n-1,a_n-2, … a₂, a₁ e a₀ são os coeficientes da função, pertencentes ao conjunto dos números reais.

Exemplos:

• f(x) = 2x + 3

• f(x) = – x² + 2x + 4

• f(x) = 5x³ + x² – 3x + 8

• f(x) = – 3x⁹ + 7x² – 3

Grau de uma função polinomial

Para saber qual é o grau da função polinomial, analisamos o grau do polinômio que descreve essa função. O grau do polinômio é o maior expoente que existir na incógnita. O grau da função polinomial é fundamental para compreender melhor qual é o comportamento da função.

• Função polinomial do 1º grau ou função afim

A função polinomial do 1º grau é conhecida também como função afim, e a sua lei de formação é f(x) = ax+b.

Exemplos:

• f(x) = x – 2

• f(x) = – 5x + 8

• f(x) = x

• f(x) = 4 – 2x

Leia também: Estudo do sinal da função afim

• Função polinomial do 2º grau ou função quadrática

A função polinomial do 2º grau é também conhecida como função quadrática. Para que uma função polinomial seja do 2º grau, é necessário que a sua lei de formação seja do tipo f(x) = ax² + bx + c.

Exemplos:

• f(x) = x² – x + 1

• f(x) = – 2x² + 5x

• f(x) = 7x² – 49

• f(x) = --3x²

• Função polinomial do 3º grau ou função cúbica

A função polinomial do 3º grau é conhecida também como função cúbica. Para que a função seja cúbica, sua lei de formação deve ser f(x) = ax³ + bx² + cx + d.

Exemplos:

• f(x) = x³ – 2x² + x + 4

• f(x) = 4x³ – 9x² + x

• f(x) = – 2x³ + 3x – 5

• f(x) = – 8x³

• Função polinomial do 4º grau

Conhecemos como função polinomial do 4º grau a função cuja lei de formação é um polinômio do tipo f(x) = ax⁴ + bx³ + cx² + dx + e.

Exemplos:

• f(x) = 3x⁴ + 2x³ – x² + x + 1

• f(x) = 5x⁴ + x³ – 2x

• f(x) = x⁴ – x² + 2

• f(x) = – x⁴

• Função polinomial do 5º grau

Utilizando a mesma ideia aplicada nas anteriores, a lei de formação da função polinomial do 5º grau é f(x) = ax⁵ + bx⁴ + cx³ + dx² + ex + f.

Exemplos:

• f(x) = x⁵ – x⁴ + 5x³ – 2x² + x + 1

• f(x) = – 3x⁵ + 2x³ – 2

• f(x) = – x⁵ – x² + 2x

• f(x) = x⁵

• Função polinomial do 6º grau

A lei de formação de uma função polinomial do 6º grau é f(x) = ax⁶ + bx⁵ + cx⁴ + dx³ + ex² + fx + g.

Exemplos:

• f(x) = x⁶ – 3x⁵ – 2x⁴ + 5x³ – x² + 7x + 1

• f(x) = x⁶ – x⁵ + 7x³ – 2

• f(x) = x⁶– x⁵ – 5x² + x

• f(x) = x⁶

Valor numérico da função

O valor numérico da função quando x = k nada mais é do que f(k). Para calculá-lo, basta substituir o valor desejado no lugar da incógnita.

Exemplo:

Dada a função f(x) = x⁴ + x³ – 3x² – 5x + 1, calcule f(2).

Resolução:

Queremos o valor numérico da função quando x =2, então, substituindo na lei de formação, temos que:

f(2) = 2⁴ + 2³ – 3·2² – 5·2 + 1

f(2) = 16 + 8 – 3·4 – 10 + 1

f(2) = 24 – 12 – 10 + 1

f(2) = 12 – 10 + 1

f(2) = 2 + 1

f(2) = 3

Leia também: Estudo da variação do sinal de uma função do 2° grau

Gráfico da função polinomial

Quando encontramos o valor numérico da função para determinados valores de x, é possível representar esse valor numérico no plano cartesiano como pontos do tipo (k, f(k)). Ao fazer a representação de vários pontos no plano cartesiano, é possível compreender o comportamento da função.

• Gráfico de uma função polinomial do 1º grau

Funções do tipo f(x) = ax +b possuem como gráfico uma reta. Vejamos a representação gráfica da função f(x) = x+1:

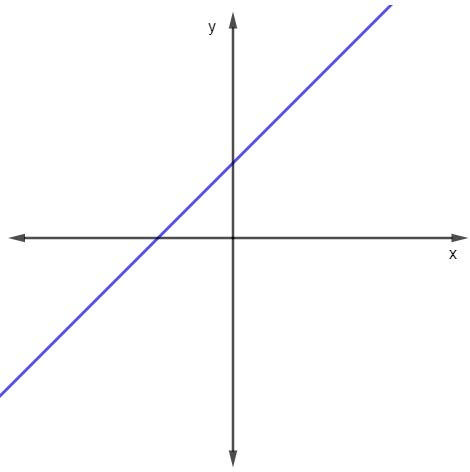
• Gráfico de uma função polinomial do 2º grau

Funções do segundo grau possuem como gráfico uma parábola. Vejamos o gráfico da função f(x) = x² – 2:

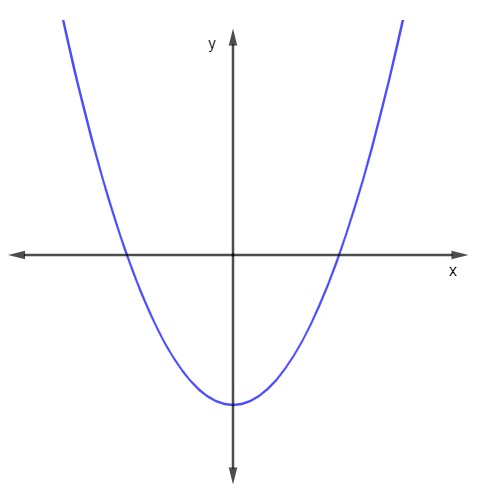
• Gráfico de uma função do 3º grau

O gráfico de uma função do 3º grau é conhecido como cúbica. Vejamos o exemplo do gráfico da função f(x) = x³ – 2x:

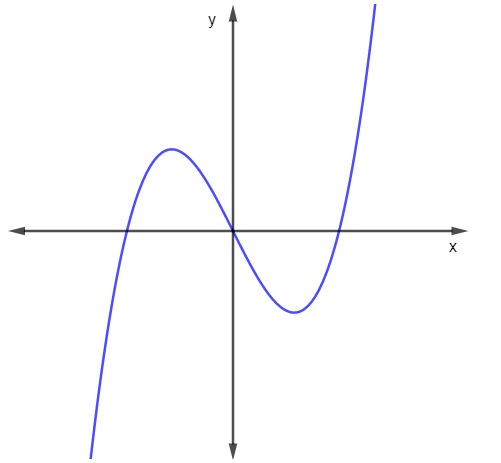
Igualdade de polinômios

Para comparar dois polinômios que possuem mesma variável, é necessário que os termos do mesmo grau tenham o mesmo coeficiente.

Exemplo:

Dados os polinômios p(x) e q(x), encontre o valor de a, b e c para que p(x) = q(x).

• p(x) = (a – 5) x² + 4x + c

• q(x) = – 2x² + (b – 1)x – 5

Resolução:

Para que p(x) seja igual a q(x), primeiro vamos igualar o coeficiente de x²:

a – 5 = – 2

a = – 2 + 5

a = 3

Agora igualamos os coeficientes de x:

b – 1 = 4

b = 4 + 1

b = 5

Por fim, falta igualar os termos independentes:

c = – 5

Leia também: Equação polinomial — expressão envolvendo um polinômio e uma igualdade

Operações com polinômios

Para trabalhar com funções polinomiais, é importante o domínio das operações básicas entre polinômios.

• Adição de polinômios

Na adição de polinômios, fazemos uma simplificação dos termos semelhantes.

Exemplo:

Calcule p(x) + q(x) sabendo que p(x) = 2x² + 3x – 5 e q(x) = x³ + 3x² + x + 2.

Resolução:

p(x) + q(x) = (2x² + 3x – 5) + (x³ + 3x² + x + 2)

Somando os termos semelhantes, temos que:

2x² + 3x² = 5x²

3x + x = 4x

– 5 + 2 = – 3

Note também que não há nenhum termo semelhante ao x³, então a soma dos polinômios será:

p(x) + q(x) = x³ + 5x² +4x – 3

• Subtração de polinômios

A subtração é análoga à adição, ou seja, vamos simplificar os termos semelhantes; porém, antes, é necessário trocar o sinal de todos os termos do segundo polinômio.

Exemplo:

Calcule p(x) – q(x) sabendo que p(x) = 2x² + 3x – 5 e q(x) = x³ + 3x² + x + 2.

Resolução:

p(x) – q(x) = (2x² + 3x – 5) – (x³ + 3x² + x + 2)

Primeiro vamos escrever o oposto de cada um dos termos do segundo polinômio.

p(x) – q(x) = (2x² + 3x – 5) + (– x³ – 3x² – x – 2)

Agora, simplificando os termos semelhantes:

2x² – 3x² = – x²

3x – x = 2x

– 5 – 2 = – 7

Não há nenhum termo semelhante ao – x³, então a subtração será:

p(x) – q(x) = – x³ – x² + 2x – 7

• Multiplicação de polinômios

Para realizar a multiplicação de polinômios, utilizamos a propriedade distributiva.

Exemplo:

Dados os polinômios p(x) = 2x + 1 e q(x) = x – 3, calcule p(x) · q(x).

Resolução:

p(x) · q(x) = (2x + 1) ( x – 3)

p(x) · q(x) = 2x² – 6x + x – 3

Agora, se possível, simplificamos os termos semelhantes:

p(x) · q(x) = 2x² – 5x – 3

• Divisão de polinômios

Para realizar a divisão entre dois polinômios, utilizamos o método de chaves, que é o mesmo utilizado para dividir dois números quaisquer.

Exemplo:

Calcule a divisão entre p(x) = x² – x + 6 e q(x) = x – 3.

Resolução:

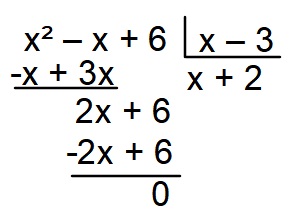
Leia também: Função exponencial — a função que sua variável está no expoente

Exercícios resolvidos sobre função polinomial

Questão 1

O valor de uma corrida de um táxi é calculado por meio de uma função que relaciona a distância percorrida d em quilômetros, além da taxa fixa de R$ 4,50, conhecida como bandeira fixa. Sabendo que o valor por km rodado é de R$ 2,75, o valor pago por esse cliente após rodar 8 km é de:

A) R$ 22,00
B) R$ 25,50
C) R$ 26,50
D) R$ 27,00
E) R$ 54,00

Resolução:

Alternativa C.

Primeiro vamos descrever a função que relaciona o valor pago V pela quantidade de km percorridos. Sabemos que são cobrados 2,75 por km rodado, além da taxa fixa de 4,50.

V(d) = 2,75d + 4,50

Queremos o valor numérico para d = 8:

V(8) = 2,75 · 8 + 4,50

V(8) = 22 + 4,50

V(8) = 26,50

Questão 2

Das alternativas a seguir, marque aquela que contém uma função polinomial.

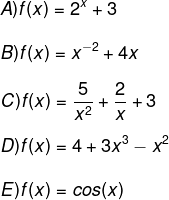
Resolução:

Alternativa D.

• Na alternativa A, a incógnita está no expoente, o que faz com que ela seja uma função exponencial.

• Na alternativa B, o expoente de x é negativo.

• Na alternativa C, x está no denominador da fração, o que faz com que as funções não sejam polinomiais.

• Por fim, na alternativa E, temos uma função trigonométrica.