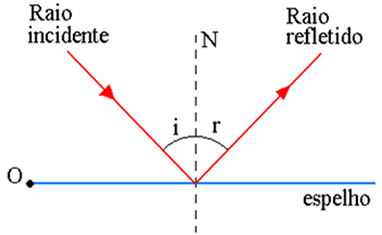
Na figura acima temos um raio de luz que incide sobre um espelho fixo no ponto O e que é refletido formando um ângulo r com a reta normal ao espelho. Considere um raio incidente no espelho plano situado na posição inicial 1. Rr1 é respectivo ao raio refletido. Girando o espelho, de um ângulo α, em relação a um eixo contido no próprio plano do espelho, o mesmo raio incidente Ri individualiza o raio refletido Rr2, agora com o espelho na posição 2, conforme ilustra a figura abaixo.
A figura acima mostra o esquema da trajetória dos raios, onde:
I1 – ponto de incidência de Ri no espelho, na posição 1
2 – ponto de incidência de Ri no espelho, na posição 2
α – ângulo de rotação do espelho
Δ – o ângulo de rotação dos raios refletidos é o ângulo entre Rr1 e Rr2
I – ponto de intersecção dos prolongamentos de Rr1 e Rr2
Sabendo que a soma dos ângulos internos de um triângulo vale 180°, temos:
∆+2a+(180°-2b)=180°
∆ =2b-2a
∆ =2(b-a)(I)
α=b-a (II)
Substituindo (II) em (I), temos:
∆ =2α
Sendo assim, podemos definir que o ângulo de rotação dos raios refletidos é o dobro do ângulo de rotação do espelho.
