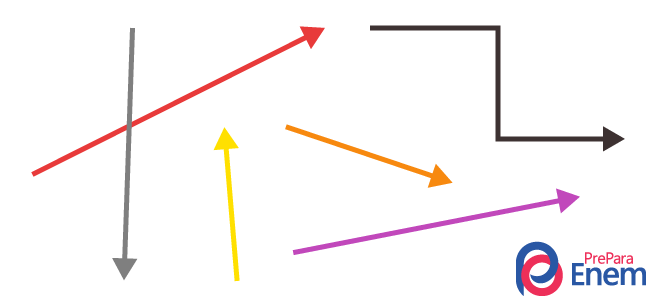
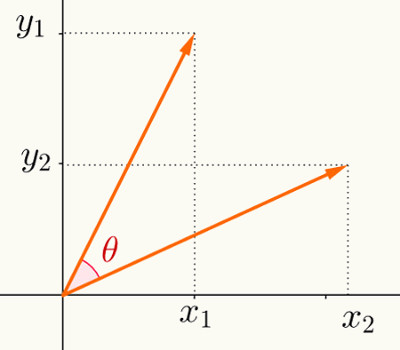As operações com vetores são operações matemáticas (como soma, subtração, multiplicação e decomposição vetorial) efetuadas com vetores em uma mesma direção, vetores perpendiculares e vetores oblíquos, originando um vetor resultante. Os vetores são instrumentos matemáticos para representação das grandezas vetoriais.
Leia também: Afinal, o que são vetores?
Tópicos deste artigo
- 1 - Resumo sobre operações com vetores
- 2 - O que são vetores?
- 3 - Quais são as operações com vetores?
- 4 - Exercícios resolvidos sobre operações com vetores
Resumo sobre operações com vetores
-
As operações com vetores são operações algébricas que podemos realizar com diferentes tipos de vetores.
-
São elas: soma, subtração, multiplicação por um número real e decomposição vetorial.
-
Vetor resultante é o que resulta das operações com vetores.
-
Na soma e subtração de vetores perpendiculares, usamos o teorema de Pitágoras, para encontrar o módulo do vetor resultante, e a regra do paralelogramo, para encontrar a orientação dele.
-
Na soma e subtração de vetores na mesma direção, realizamos uma soma dos valores numéricos dos vetores para calcular o módulo do vetor resultante.
-
Na multiplicação de um vetor por um número real, fazemos o produto do tamanho do vetor por um número real.
-
Na decomposição vetorial, encontramos as projeções na horizontal e vertical de um vetor.
O que são vetores?
Os vetores são segmentos de reta similares a flechas que representam as grandezas vetoriais, caracterizando-as com módulo, direção e sentido.
-
Módulo de um vetor: é o tamanho ou intensidade numérica da grandeza vetorial, representado, por exemplo, como \(\left| \vec{a} \right| \) ou a.
-
Direção de um vetor: é a orientação do vetor em horizontal, vertical ou diagonal.
-
Sentido de um vetor: é para onde o vetor aponta, podendo ser para cima, para baixo, para a direita, para a esquerda, para o norte, para o sul, para o oeste, para o leste, para o noroeste e outros.
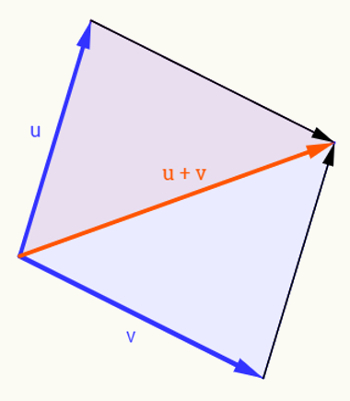
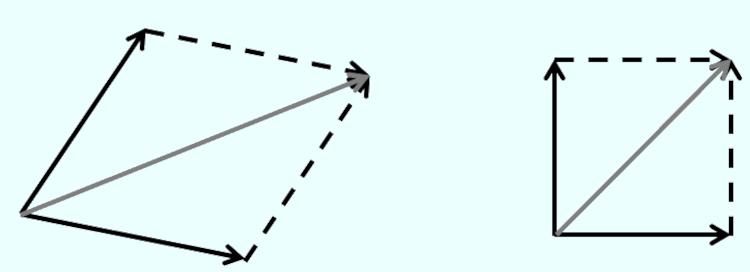
Importante: O sentido e a direção de um vetor, em alguns casos, só são descobertos por meio da regra do paralelogramo, que consiste em juntar os vetores e fazer as suas projeções (setas pontilhadas), formando um quadrado ou paralelogramo, em que a diagonal entre os dois vetores é o vetor resultante (vetor cinza), conforme descrito na imagem abaixo:
Quais são as operações com vetores?
É possível realizar algumas operações algébricas com os vetores, como soma, subtração, multiplicação por um número real e decomposição vetorial, que resultam em um vetor chamado de resultante.
→ Soma e subtração de vetores perpendiculares
Os vetores perpendiculares são aqueles que, quando somados ou subtraídos (quando um vetor tem sentido oposto), fazem um ângulo de 90° (ângulo reto) ou 270º entre eles, gerando um vetor resultante com orientação dada pela regra do paralelogramo e intensidade (módulo ou tamanho), calculada pela fórmula de Pitágoras:
\(\text{hipotenusa}^2 = \text{cateto}_1^2 + \text{cateto}_2^2 \)
-
Exemplo:
Calcule o vetor resultante da soma de um vetor \(\vec v\), com módulo de 3 unidades e orientação vertical para cima, com outro vetor \(\vec u\), com módulo de 4 unidades e orientação horizontal para direita.
Resolução:
Primeiramente, desenharemos os dois vetores informados, e, usando a regra do paralelogramo, encontraremos o vetor resultante, como representado abaixo:
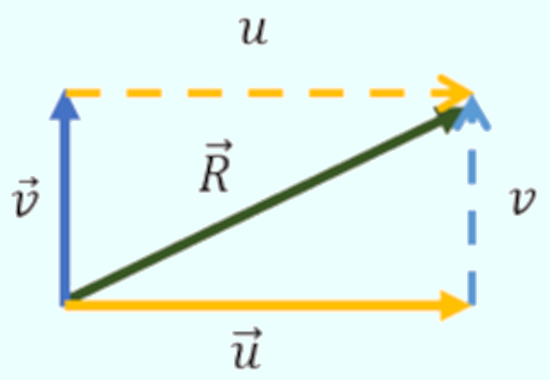
Depois, calcularemos o tamanho do vetor resultante por meio do teorema de Pitágoras:
\(\text{hipotenusa}^2 = \text{cateto}_1^2 + \text{cateto}_2^2 \)
No qual a hipotenusa indica o tamanho do vetor resultante, e os catetos, os tamanhos dos outros vetores:
\(\)\({R} ^ {2} = {u} ^ {2} + {v} ^ {2}\)
\({R} ^ {2} = {4} ^ {2} + {3} ^ {2}\)
\({R} ^ {2} =16+9\)
\({R} ^ {2} =25\)
\(R = \sqrt{25u} \)
\(R =5 u\)
O tamanho do vetor resultante é de 5 unidades, o sentido é nordeste e a direção é diagonal.
→ Soma e subtração de vetores na mesma direção
Os vetores na mesma direção, quando somados ou subtraídos (quando um vetor tem sentido oposto), fazem um ângulo de 180° (ângulo raso), 0° ou 360º entre eles, gerando um vetor resultante com direção igual à dos vetores, sentido igual ao vetor de maior tamanho e intensidade (módulo ou tamanho) calculada pela soma deles:
-
Exemplo:
Calcule o vetor resultante da soma de um vetor \(\vec v\), com módulo de 1 unidade e orientação horizontal para a direita, com outro vetor \(\vec u\), com módulo de -3 unidades e orientação horizontal para direita.
Resolução:
Primeiramente, desenharemos os dois vetores informados, alterando o sentido do vetor \(\vec u\), e encontraremos o vetor resultante, como representado abaixo:
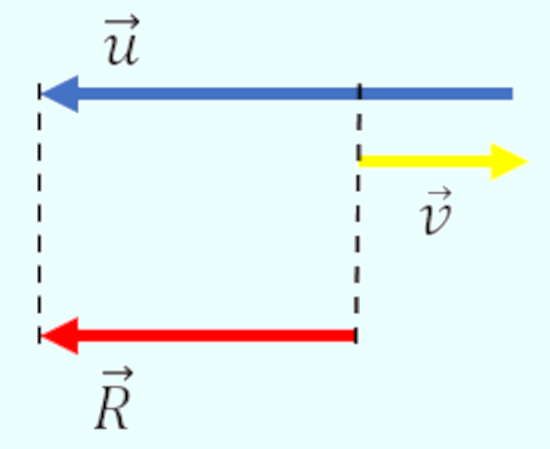
Depois, calcularemos o tamanho do vetor resultante por meio de uma adição:
\(\vec{R} = \vec{v} + \vec{u} \)
\(\vec{R} = 1 + (-3) \)
\(\vec{R} = -2u \)
O tamanho do vetor resultante é de 2 unidades, o sinal negativo indica que ele tem o sentido contrário ao do vetor \(\vec v\), o de menor tamanho (3 > 1), então o seu sentido é para a esquerda e a direção é horizontal.
→ Soma e subtração de vetores oblíquos
Os vetores oblíquos são aqueles que, quando somados ou subtraídos (quando um vetor tem sentido oposto), fazem um ângulo de 0°, 90°, 180°, 270º ou 360º entre eles, gerando um vetor resultante com orientação dada pela regra do paralelogramo e intensidade (módulo ou tamanho), calculada pela lei dos cossenos:
\(\text{hipotenusa}^2 = \text{cateto}_1^2 + \text{cateto}_2^2 - 2 \cdot \text{cateto}_1 \cdot \text{cateto}_2 \cdot \cos{\theta} \)
-
Exemplo:
Calcule o vetor resultante da soma de um vetor \(\vec v\), com módulo de 5 unidades e orientação a noroeste, com outro vetor \(\vec u\), com módulo de 2 unidades e orientação horizontal para leste, sabendo que o ângulo formado pela sua combinação é de 60°.
Resolução:
Primeiramente, desenharemos os dois vetores informados, e, usando a regra do paralelogramo, encontraremos o vetor resultante, como representado abaixo:
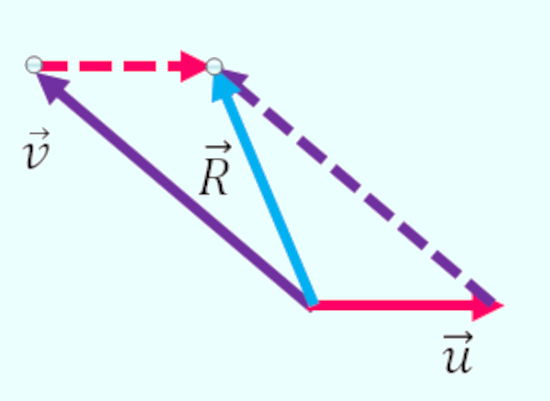
Depois, calcularemos o seu tamanho por meio da lei dos cossenos:
\(\text{hipotenusa}^2 = \text{cateto}_1^2 + \text{cateto}_2^2 - 2 \cdot \text{cateto}_1 \cdot \text{cateto}_2 \cdot \cos{\theta} \)
No qual a hipotenusa indica o tamanho do vetor resultante, e os catetos, os tamanhos dos outros vetores:
\(R^2 = u^2 + v^2 - 2 \cdot u \cdot v \cdot \cos{\theta} \)
\(R^2 = (-2)^2 + 5^2 - 2 \cdot (-2) \cdot 5 \cdot \cos{60^\circ} \)
\({R} ^ {2} = 4 +25+20\cdot0,5\)
\({R} ^ {2} = 4+25+ 10\)
\({R} ^ {2} = 39\)
\(R = \sqrt{39} \)
\(R≈6,2 u\)
O tamanho do vetor resultante é de aproximadamente 6,2 unidades, o sentido é noroeste e a direção é diagonal.
→ Multiplicação de um vetor por um número real
Um vetor pode ser multiplicado por um número real, gerando um vetor resultante com direção igual ao vetor original, sentido dependendo do produto do vetor original pelo número, e intensidade (módulo ou tamanho) calculada pelo produto do vetor original com o número real, representado pela fórmula:
\(v_{\text{novo}} = n \cdot \vec{v} \)
-
Exemplo:
Dado um vetor \(\vec {v}\), com módulo de 120 unidades, direção vertical e sentido para cima, qual será seu valor se o multiplicarmos pelo número real -6?
Resolução:
A direção será vertical e o sentido para baixo (sinal negativo) respectivamente; mas seu módulo mudará e terá valor igual a:
\(v_{\text{novo}} = n \cdot \vec{v} \)
\(v_{\text{novo}} = -6 \cdot 120 \)
\(v_{\text{novo}} = -720 \, \text{u} \)
O módulo ou tamanho do vetor novo é de -720 unidades.
→ Decomposição vetorial
A decomposição vetorial é um ferramenta matemática empregada quando se precisa descobrir as componentes x e y (projeções ou sombras) de um vetor. Basicamente, encontra-se os vetores originais sabendo apenas o vetor resultante.
Para isso, é necessário identificar a posição do vetor, desenhar suas componentes, fazer suas projeções e identificar se o ângulo está na horizontal ou na vertical, como no exemplo abaixo, em que o vetor original é o A e as suas componentes são \({A_x}\) e \({A_y}\):
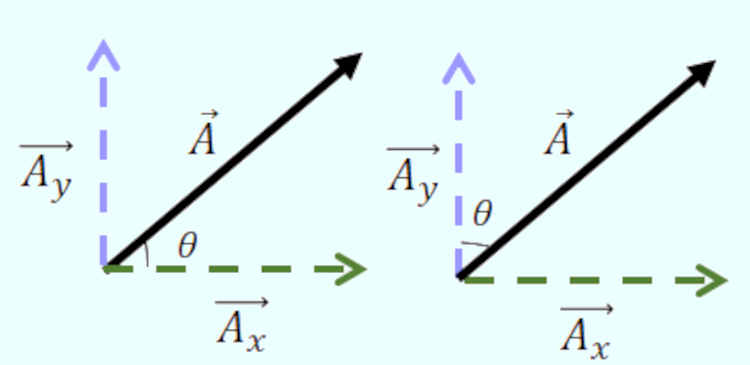
Quando o ângulo está na horizontal (imagem à esquerda), a componente x e a componente y serão calculadas pelas fórmulas:
\(A_x = A \cdot \cos{\theta} \)
\(A_y = A \cdot \ sen{\theta} \)
Quando o ângulo está na vertical (imagem à direita), a componente x e a componente y serão calculadas pelas fórmulas:
\(A_x = A \cdot \ sen{\theta} \)
\(A_y = A \cdot \cos{\theta} \)
-
Exemplo:
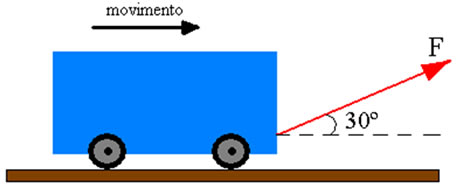
Calcule as componentes x e y da força F, de intensidade 200 N com orientação a nordeste e que faz um ângulo de 60° com a horizontal. Conside \(sen 60° = 0,9\) e
\(cos 60° = 0,5\).
Resolução:
Primeiramente, desenharemos o vetor F informado e faremos a sua componente na vertical \({F_y}\) e sua componente horizontal
\({F_x}\). Depois, encontraremos as suas projeções pela regra do paralelogramo para descobrir em qual delas usaremos cosseno e seno.
Em seguida, calcularemos o módulo da componente horizontal \({F_x}\), que, nesse caso, dá-se pela fórmula:
\(F_x = F \cdot \cos{60^\circ} \)
\(F_x = 200 \cdot 0,5 \)
\(F_x = 100 \, \text{N} \)
Depois, calcularemos o módulo da componente vertical \({F_y}\), que, nesse caso, dá-se pela fórmula:
\(F_y = F \cdot \sin{60^\circ} \)
\(F_y = 200 \cdot 0,9 \)
\(F_y = 180 \, \text{N} \)
Acesse também: O que é a velocidade vetorial?
Exercícios resolvidos sobre operações com vetores
Questão 1
Os vetores \(\vec x\), \(\vec y\)
e
\(\vec z\) têm módulos iguais a 1, 2 e 3 respectivamente. Com base nessas informações, calcule o módulo do vetor
\(\vec{a} = \vec{x} - \vec{y} \) e do vetor
\(\vec{b} = \vec{a} + \vec{z} \).
A) -1, 2
B) 1, -2
C) 1, 2
D) -1, -2
E) 0, 2
Resolução:
Alternativa A
Calcularemos o módulo do vetor \(\vec a\) pela expressão:
\(\vec{a} = \vec{x} - \vec{y} \)
\(\vec{a} = 1 - 2 \)
\(\vec{a} = -1 \)
E calcularemos o módulo do vetor por meio da expressão:
\(\vec{b} = \vec{a} + \vec{z} \)
\(\vec{b} = -1 + 3 \)
\(\vec{b} = 2 \)
Questão 2
(Enem) A força de atrito é uma força que depende do contato entre corpos. Pode ser definida como uma força de oposição à tendência de deslocamento dos corpos e é gerada devido a irregularidades entre duas superfícies em contato. Na figura, as setas representam forças que atuam no corpo e o ponto ampliado representa as irregularidades que existem entre as duas superfícies.
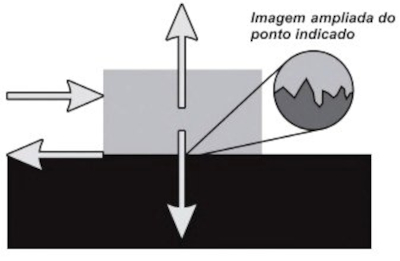
Na figura, os vetores que representam as forças que provocam o deslocamento e o atrito são, respectivamente:
A) ![]()
B) 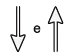
C) ![]()
D) 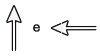
E) 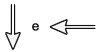
Resolução:
Alternativa A
Os vetores que representam as forças que provocam o deslocamento e o atrito são aqueles que ocorrem na direção horizontal, em sentidos opostos.
Fontes
HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Mecânica. 8. ed. Rio de Janeiro, RJ: LTC, 2009.
NUSSENZVEIG, Herch Moysés. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Editora Blucher, 2015.