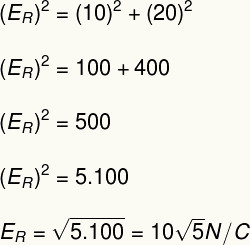O campo elétrico é uma grandeza vetorial que mede o módulo da força elétrica por unidade de carga em cada ponto do espaço ao redor de uma carga elétrica. Quanto maior for o campo elétrico em algum ponto do espaço, maior será a intensidade da força elétrica que atua sobre as cargas.
Veja também: Força elétrica
Tópicos deste artigo
- 1 - Campo elétrico de uma carga puntiforme
- 2 - Campo elétrico uniforme
- 3 - Linhas de campo elétrico
- 4 - Atração e repulsão elétrica
- 5 - Vetor campo elétrico
- 6 - Módulo do campo elétrico resultante
- 7 - Campo elétrico e potencial elétrico
- 8 - Exercícios sobre campo elétrico
Campo elétrico de uma carga puntiforme
Para calcularmos o campo elétrico de uma carga puntiforme, isto é, de uma carga com dimensões desprezíveis, utilizamos a seguinte equação:
![]()
E – campo elétrico
Q – carga geradora do campo elétrico
q – carga de prova
r – distância do ponto até a carga geradora
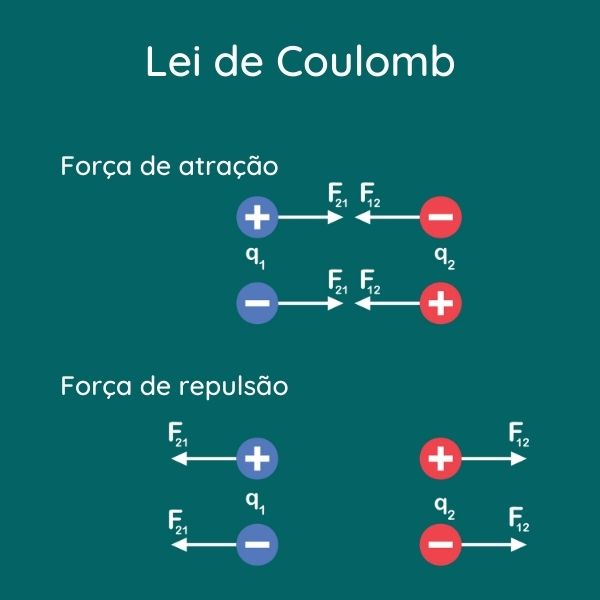
A definição de campo elétrico está intimamente relacionada à força elétrica entre as cargas Q e q. A força elétrica entre duas cargas puntuais é dada pela lei de Coulomb:
![]()
Veja também: Experimento de Coulomb
Ao unirmos a lei de Coulomb com a própria definição de campo elétrico, teremos a seguinte relação:
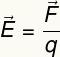
Campo elétrico uniforme
O campo elétrico das cargas positivas é radial, isto é, propaga-se na direção da reta que liga um ponto do espaço à carga que o origina. Além disso, seu sentido é para fora, ou seja, o campo elétrico das cargas positivas emerge delas. Observe as figuras abaixo:
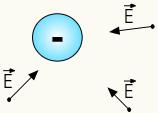
Campo elétrico das cargas negativas
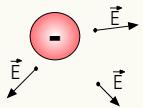
Campo elétrico das cargas positivas
Linhas de campo elétrico
Podemos determinar o formato do campo elétrico gerado por uma carga ou por uma distribuição de cargas usando as linhas de campo elétrico. Cada ponto do espaço apresenta um módulo, uma direção e um sentido de campo elétrico.
Para representarmos o campo elétrico, usamos um artifício geométrico chamado linhas de força. Essas linhas são desenhadas de forma que sua tangente indique a direção do campo elétrico.
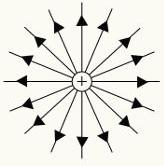
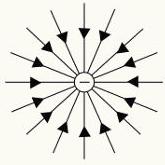
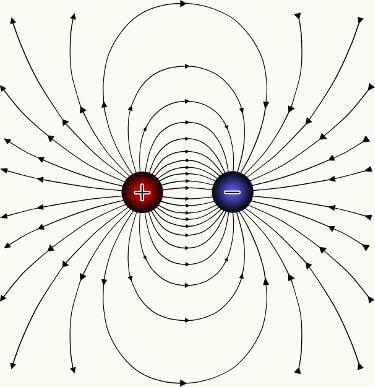
Linhas de força das cargas elétricas positiva e negativa.
Atração e repulsão elétrica
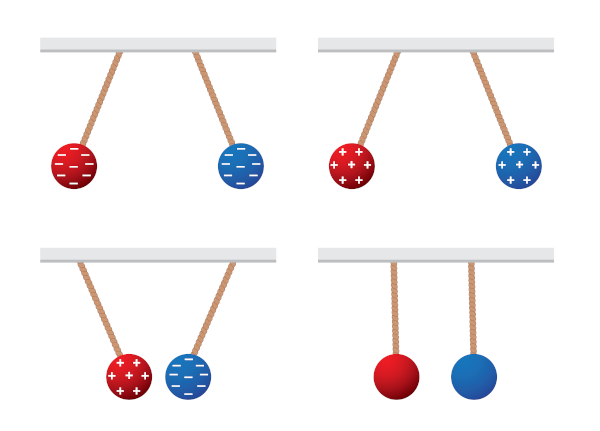
A atração ou a repulsão elétrica decorre da componente resultante do campo elétrico ponto a ponto. A tendência das cargas elétricas é repelirem-se quando seus sinais forem iguais e atraírem-se quando seus sinais forem diferentes.
Na figura abaixo, temos uma carga negativa geradora de campo elétrico e duas cargas de prova que sofrem, respectivamente, atração e repulsão eletrostática, de acordo com seus sinais:
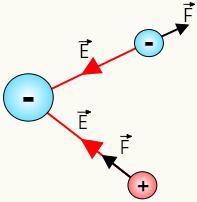
Vetor campo elétrico
Por apresentar módulo, direção e sentido, o campo elétrico é descrito por um vetor. Como todo vetor, o campo elétrico pode ser escrito em termos de suas componentes, nas direções x, y e z. Usando a notação i, j e k para denotar cada uma dessas direções, temos:
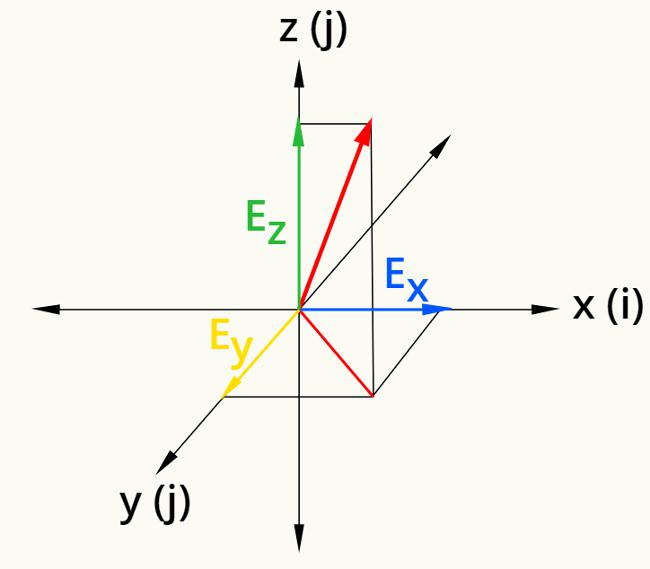
Ex – direção x do campo elétrico
Ey – direção y do campo elétrico
Ez – direção z do campo elétrico
Assim, o vetor campo elétrico pode ser escrito da seguinte forma:
![]()
Módulo do campo elétrico resultante
Como o campo elétrico é uma grandeza vetorial, pode ser necessário calcular o módulo do vetor resultante da soma de campos elétricos. Nessa seção, veremos como é possível calcular o valor numérico do campo elétrico resultante em um ponto do espaço.
Resultante de campos elétricos paralelos
Quando dois vetores de campo elétrico encontrarem-se paralelos um em relação ao outro (ângulo de 0º), deveremos somá-los:
![]()
ER – campo elétrico resultante
E1 – campo elétrico 1
E2 – campo elétrico 2
Resultante de campos elétricos opostos
Quando houver dois vetores de campo elétrico na mesma direção, porém com sentidos opostos (ângulo de 180º), é possível calcular o módulo do campo elétrico resultante por meio da diferença entre os módulos desses campos elétricos:
![]()
Resultante de campos elétricos perpendiculares
Nos casos em que houver dois campos elétricos perpendiculares entre si, ou seja, quando os dois vetores cruzarem-se com ângulos de 90º, o módulo do campo elétrico resultante deles poderá ser calculado por meio do teorema de Pitágoras. Observe:
![]()
Resultante de campos elétricos oblíquos
Se o ângulo formado entre dois vetores de campo elétrico for diferente de 0º, 90º, 180º e 270º, utilizaremos a equação abaixo para calcular o módulo do campo elétrico resultante:
![]()
α – ângulo entre os vetores de campo elétrico
Campo elétrico e potencial elétrico
Diferentemente do campo elétrico, o potencial elétrico é escalar. Essa grandeza mede a energia potencial elétrica por unidade de carga, ou seja, a quantidade de trabalho realizado pelo campo elétrico por unidade de carga. A unidade de potencial elétrico, de acordo com o Sistema Internacional de Unidades (SI), é o volt (V).
É possível estabelecer uma relação matemática entre o campo elétrico gerado em um ponto do espaço e o potencial elétrico gerado por ele a uma distância d em relação a esse ponto. Observe:
![]()
U – potencial elétrico
E – campo elétrico
d – distância
Exercícios sobre campo elétrico
1) Uma carga elétrica puntiforme de 10 mC é colocada no vácuo a uma distância de 0,5 m de um ponto P do espaço. Determine o módulo do campo elétrico gerado por essa carga no ponto P.
Dados
k0 = 9.109 N.m²/C²
Resolução
A fórmula usada para calcular o módulo do campo elétrico gerado por cargas puntiformes é mostrada abaixo:
![]()
Antes de substituirmos os valores fornecidos no enunciado, precisamos lembrar que 10 mC equivalem a 10.10-3 C. Dessa forma, teremos o seguinte cálculo:
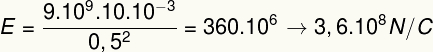
2) Dois vetores de campo elétrico perpendiculares entre si, de módulos iguais a 10 N/C e 20 N/C, cruzam-se em uma determinada posição do espaço. Determine o módulo do campo elétrico resultante nesse ponto.
Resolução
Como os dois vetores de campo elétrico descritos no exercício são perpendiculares entre si, utilizaremos o teorema de Pitágoras para calcular o módulo do campo elétrico resultante. Confira o cálculo feito abaixo: