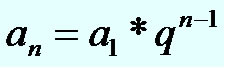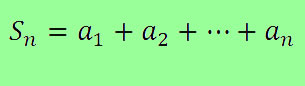A soma dos termos de uma progressão aritmética (PA) é calculada utilizando uma fórmula que nos permite encontrar a soma de todos os termos da progressão. Para compreender como é feita essa soma, é importante lembrar que uma progressão aritmética é uma sequência de números em que a diferença entre cada par de termos consecutivos é sempre constante.
Leia também: Como fazer a soma dos termos de uma PG?
Tópicos deste artigo
- 1 - Resumo sobre soma dos termos de uma PA
- 2 - Como identificar os termos de uma PA?
- 3 - Fórmula da soma dos termos de uma PA
- 4 - Como fazer a soma dos termos da PA?
- 5 - Soma dos termos consecutivos de uma PA
- 6 - Origem da soma dos termos de uma PA
- 7 - Exercícios resolvidos sobre soma dos termos de uma PA
Resumo sobre soma dos termos de uma PA
- A soma dos termos de uma PA é calculada utilizando uma fórmula que nos permite encontrar a soma de todos os termos dessa sequência matemática.
- Para fazer essa soma, é preciso identificar os termos de uma progressão aritmética (PA), o que envolve reconhecer os elementos fundamentais que compõem essa sequência matemática.
- A soma dos n primeiros termos de uma progressão aritmética (PA) é calculada pela seguinte fórmula:
\(S_n=\frac{(a_1+a_n)n}{2}\)
- A soma dos termos consecutivos de uma PA, começando por outro termo que não é o primeiro, é dada pela seguinte fórmula:
\(S_{(t-k)}=\frac{(a_k+a_t)\cdot(t-k)}{2}\)
- A origem da soma dos termos de uma PA se deu com Carl Friedrich Gauss.
Como identificar os termos de uma PA?
Para identificar os termos de uma PA, é importante compreender primeiro quando uma sequência é uma progressão aritmética (PA). Encontrar a diferença constante entre termos consecutivos é essencial para identificar a PA. Podemos obter a diferença subtraindo um termo pelo seu antecessor. Se essa diferença tiver sempre o mesmo valor, então a sequência é uma progressão aritmética e essa diferença é conhecida como razão.
Considerando a sequência de termos \(\left(2,\ 5,\ 8,\ 11,\ 14,\ 17,\ 20...\right)\), temos que \(5-2=3, 8-5=3, 11-8=3, 14-11=3, 17-14=3 \ e \ 20-17=3\). Assim, a diferença entre dois termos consecutivos é sempre 3, logo essa é um PA de primeiro termo 2 e razão 3.
Os termos da PA são nomeados de acordo com a sua posição. Tomando a sequência anterior como exemplo, temos que:
\(\left(2,\ 5,\ 8,\ 11,\ 14,\ 17,\ 20...\right)\)
a1=2 → primeiro termo
a2=5 → segundo termo
a3=8 → terceiro termo
Existe uma fórmula que nos permite encontrar qualquer termo da progressão, chamada de termo geral da PA:
\(a_n=a_1+\left(n-1\right)r\)
Nela, n é o termo desejado, a1 é o primeiro termo da progressão e r é a razão da progressão.
- Exemplo:
Dada a sequência (9, 11, 13, 15, 17, 19 ...), identifique o valor do 8º termo dessa progressão.
Resolução:
Primeiro calcularemos a razão. Note que 11 – 9 = 2, e que isso se repete para quaisquer dois termos, ou seja, r = 2. Sabemos que a razão é 2, e que o primeiro termo é 9. Para calcular o termo a8, temos que:
\(a_8=9+\left(8-1\right)2\)
\(a_8=9+7\cdot2\)
\(a_8=9+14\)
\(a_8=23\)
Fórmula da soma dos termos de uma PA
Vamos entender o raciocínio a partir do qual temos a fórmula da soma dos termos de uma PA. Para isso, vamos começar somando os n termos de uma PA em duas direções diferentes, a original e a reversa. Suponha que Sn seja a soma dos primeiros n termos da PA e Sn' seja a mesma soma, mas com os termos dispostos na ordem inversa:
\(S_n=a_1+a_2{+a}_3+\ldots+a_{n-2}+a_{n-1}+a_n\)
\(S_n^\prime=a_n+a_{n-1}+a_{n-2}+\ldots+a_3{+a}_2{+a}_1\)
Agora, somaremos as duas expressões termo a termo:
\(S_n+S_n^\prime=\left(a_1+a_n\right)+{(a}_2+a_{n-1})+{(a}_3+a_{n-2})+\ldots+\left(a_{n-2}+a_3\right)+\left(a_{n-1}+a_2\right)+(a_n+a_1)\)
Observe que as somas que estão aos pares entre os parênteses são iguais. Logo podemos substitui-las por \(\left(a_1+a_n\right)\), chegando ao resultado \(S_n+S_n^\prime=n⸳a1+an\). Como \(S_n=S_n^\prime\), podemos facilmente chegar à conclusão de que \(2\ ⸳ Sn=n⸳a1+an\). A partir desse raciocínio, obtemos a fórmula dos termos de uma PA:
\(S_n=\frac{(a_1+a_n)n}{2}\)
- Sn → soma dos termos da PA.
- a1 → primeiro termo a ser somado.
- an → termo genérico ou mesmo o último termo a ser somado da sequência.
Importante: Para compreender melhor a fórmula analisamos os pares de termos equidistantes, ou seja, termos com a mesma distância do primeiro termo, do último termo e do termo médio. A soma dos pares equidistantes é sempre a mesma em uma PA, essa regularidade é o que define a PA. A soma dos termos da PA leva em consideração a contribuição de cada um desses pares para a soma total.
Como fazer a soma dos termos da PA?
A soma dos n primeiros termos de uma progressão aritmética é chamada de “soma dos termos da PA” ou “soma de uma PA finita”. Para calcular a soma dos termos da PA, utilizamos a seguinte fórmula:
\(S_n=\frac{(a_1+a_n)n}{2}\)
- Exemplo 1
Encontre a soma dos 10 primeiros termos da PA (3, 7, 11, 15...).
Resolução:
Queremos a soma dos primeiros 10 termos, porém não temos o 10º. Vamos determiná-lo antes.
\(a_1=3\)
\(a_{10}=3+\left(10-1\right)\cdot4=39 (este \ é\ o \ 10º termo)\)
Utilizando a fórmula, temos \(S_{10}=\frac{\left(a_1+a_{10}\right)10}{2}\).
\(S_{10}=\frac{\left(3+39\right)10}{2}=42\cdot5=210\)
- Exemplo 2:
Encontre a soma dos 20 primeiros termos da PA (6, 9, 12, 15....).
Resolução:
Queremos a soma dos primeiros 20 termos, porém não temos o 20º. Vamos determiná-lo antes.
\(a_1=6\)
\(a_{20}=6+\left(20-1\right)\cdot3=63\ (este\ é \ o\ 20º)\)
Utilizando a fórmula, temos \(S_{20}=\frac{\left(a_1+a_{20}\right)20}{2}\).
\(S_{20}=\frac{\left(6+63\right)20}{2}=69\cdot10=690\)
Soma dos termos consecutivos de uma PA
A soma dos termos consecutivos de uma progressão aritmética (PA), nem sempre começando pelo primeiro termo, nos permite encontrar a soma de termos específicos em uma sequência aritmética, independentemente da posição em que começamos.
Imagine uma PA com o primeiro termo \(a_1\) e uma razão r. Queremos saber a soma dos termos consecutivos a partir do termo \(a_5\) até o termo \(a_15\). Para utilizarmos a fórmula dos termos de uma PA, basta considerarmos \(a_5\) como o primeiro termo e \(a_15\) como o 11º termo, ou o termo \(a_n\). Em outras palavras, deslocamos os termos em referência a 4 posições anteriores. Veja:
\(S_{11}=\frac{(a_5+a_{15})\cdot11}{2}\)
Essa estratégia é valiosa quando desejamos calcular a soma de um subconjunto específico de termos consecutivos em uma PA, não necessariamente começando pelo primeiro termo. Ela nos permite realizar cálculos precisos e eficientes em uma variedade de contextos, desde séries financeiras até problemas de matemática e física. Generalizando o raciocínio acima, temos que a soma dos termos da PA da posição k até a posição t é dada pela seguinte fórmula:
\(S_{(t-k)}=\frac{(a_k+a_t)\cdot(t-k)}{2}\)
Origem da soma dos termos de uma PA
A soma dos termos de uma progressão aritmética (PA) tem uma longa história na matemática e remonta aos tempos antigos. A ideia de somar os termos de uma sequência com diferenças constantes foi explorada por matemáticos gregos e indianos há milhares de anos.
Na Grécia Antiga, matemáticos como Pitágoras e Euclides estudaram sequências numéricas, embora não tenham especificamente abordado as progressões aritméticas como as conhecemos hoje. No entanto, o pensamento sobre sequências e padrões matemáticos era um campo de estudo importante. No mundo indiano, séculos antes, matemáticos como Aryabhata e Brahmagupta também investigaram padrões numéricos e sequências, incluindo algumas com diferenças constantes. Eles desenvolveram métodos para calcular a soma dos termos de tais sequências.
A formulação da fórmula geral para a soma dos termos de uma PA, como a conhecemos hoje, é creditada principalmente a Carl Friedrich Gauss, um matemático alemão do final do século XVIII e início do século XIX. A história conta que, quando Gauss era criança, ele rapidamente somou os números inteiros de 1 a 100 percebendo que poderia agrupar os termos em pares e que a soma de cada par era constante (101). Então multiplicou esse valor pela metade do número de pares (50) para obter a soma total (5050).
Gauss começou a procurar um padrão e uma fórmula geral para calcular a soma de quaisquer termos de uma PA. No caso da soma de números inteiros de 1 a 100, ele dividiu a série em dois grupos: os termos menores ou iguais a 50 e os termos maiores do que 50. Gauss percebeu que esses grupos eram simétricos em relação a 50 e que a soma dos números em cada grupo era igual (1+100=2+99=3+98=4+97=5+96=…=101). Ele, então, calculou essas duas somas iguais para obter o resultado total, que é 101∙50=5050.
Isso levou Gauss a uma fórmula geral para calcular a soma dos termos de uma PA. Sua descoberta resultou na famosa fórmula da soma dos termos de uma PA \((S_n=\frac{(a_1+a_n)n}{2})\), que ainda é amplamente usada hoje.
Exercícios resolvidos sobre soma dos termos de uma PA
Questão 1
Heitor está economizando dinheiro para comprar um carro. Ele economiza R$ 200,00 a mais a cada mês. No primeiro mês, ele economizou R$ 500,00. Qual será o total economizado por Heitor após 10 meses?
A) R$ 13000,00
B) R$ 14000,00
C) R$ 11000,00
D) R$ 16000,00
E) R$ 18000,00
Resolução:
Alternativa B.
Queremos a soma dos primeiros 10 termos, porém não temos o 10º. Vamos determiná-lo antes.
\(a_1=500\)
\(a_{10}=500+\left(10-1\right)\cdot200=500+9\cdot200=2300\ (este \ é \ o\ 10º)\)
Utilizando a fórmula, temos \(S_{10}=\frac{\left(a_1+a_{10}\right)10}{2}\).
\(S_{10}=\frac{\left(500+2300\right)10}{2}=2800\cdot5=R$\ 14000,00\)
Questão 2
Uma empresa oferece um programa de bônus aos seus funcionários. No primeiro ano, um funcionário recebe um bônus de R$ 1000. A cada ano subsequente, o bônus aumenta em R$ 200 em relação ao ano anterior. Quanto um funcionário receberá de bônus ao final de 5 anos?
A) R$ 4600,00
B) R$ 6800,00
C) R$ 7000,00
D) R$ 8800,00
E) R$ 9200,00
Resolução:
Alternativa C.
Queremos a soma dos primeiros 5 termos, porém não temos o 5º. Vamos determiná-lo antes.
\(a_1=1000e\)
\(a_{10}=1000+\left(5-1\right)\cdot200=1000+4\cdot200=1800\ (este\ é \ o \ 5º)\)
Utilizando a fórmula, temos \(S_5=\frac{\left(a_1+a_5\right)5}{2}\)
\(S_{10}=\frac{\left(1000+1800\right)5}{2}=1400\cdot5=R$\ 7000,00\)
Fontes
SILVA, J. P. Progressões Aritméticas no Ensino de Matemática: Estratégias e Desafios. Revista Brasileira de Educação, vol. 32, n. 3, p. 311-328, 2007.
CARVALHO, S. Matemática: Uma Abordagem Progressiva - Volume 1. Editora Scipione, 2000.