Trabalho da força resultante

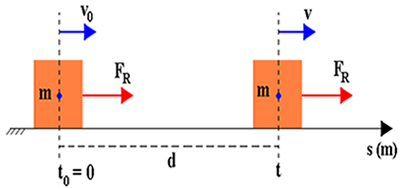
Vejamos a figura acima. Nela temos um bloco de massa m que desliza sobre uma superfície plana e horizontal. Suponhamos que o corpo de massa m tenha velocidade  e que após um período curto de tempo atue sobre o corpo uma força resultante cuja intensidade vale . Pela figura, podemos verificar que tal força é constante e paralela à velocidade inicial do corpo. Caso venhamos a manter as condições iniciais, em um instante qualquer o corpo passa a possuir uma velocidade  e terá percorrido uma distância , como mostra a figura acima.

O trabalho realizado pela força resultante constante ao longo do deslocamento pode ser determinado da seguinte maneira:

τ= F_R.d.cos0°, onde  cos0°=1

τ= F_R.d

De acordo com a Segunda Lei de Newton, temos que o módulo da força resultante possui o seguinte valor:

F_R= m . a⇒ τ = m . a . d (I)

Podemos reescrever a equação denominada equação de Torricelli da seguinte maneira:

v²= v₀²+2 .a.d 

v²- v₀²=2.a.d

Substituindo a equação (II) na equação (I), obtém-se, finalmente,

τ_FR =m .  a .  d

A grandeza física escalar  que temos como resultado da operação matemática, procede do cálculo do trabalho e está ligada ao movimento do corpo. Por esse motivo é que ela passou a ser chamada de energia cinética do corpo. Sendo assim, podemos defini-la da seguinte forma:

Quando um corpo de massa m se move com velocidade v, em relação a um determinado referencial adotado, dizemos que o corpo possui energia cinética. A energia cinética é representada por E_c, e pode ser determinada através da seguinte relação:

Acima podemos ver a equação (III). Na Física, essa equação é conhecida como Teorema da Energia Cinética. Enunciamos esse teorema da seguinte maneira:

- O trabalho da força resultante que age sobre um objeto (corpo) em um determinado intervalo de tempo é igual à variação da energia cinética naquele intervalo de tempo. Dessa forma, podemos escrever:

τ_FR = E_Cfinal -E_Cinicial ⇒ τ_FR = ?_EC

Aproveite para conferir a nossa videoaula relacionada ao assunto: