Ao estudarmos o conceito de impulso, vimos que o impulso de uma força constante, num intervalo de tempo, é igual à variação da quantidade de movimento produzida por essa força, no intervalo de tempo Δt. Podemos estender o conceito de impulso para uma força variável. Para o caso da força variável, vamos imaginar que dividimos o intervalo de tempo em um número grande de “pequenos pedaços”, de maneira que em cada “pedaço” a força possa ser considerada constante.
Em um segundo momento, aplicamos a fórmula  a cada pedaço e depois somamos os resultados. Sabemos que esse procedimento é complexo e exige a aplicação de Cálculo Integral. Há, porém, uma situação especial que consideraremos: é o caso de uma força que tem direção constante, variando apenas o módulo ou o sentido.
a cada pedaço e depois somamos os resultados. Sabemos que esse procedimento é complexo e exige a aplicação de Cálculo Integral. Há, porém, uma situação especial que consideraremos: é o caso de uma força que tem direção constante, variando apenas o módulo ou o sentido.
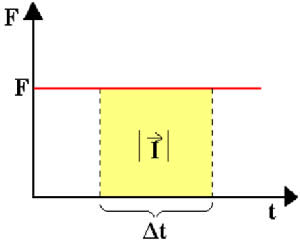
Para considerar esse caso, partimos do caso simples em que a força  é constante. No gráfico do módulo de
é constante. No gráfico do módulo de  em função do tempo, representado na figura acima, a área sombreada (em amarelo) é numericamente igual ao módulo do impulso.
em função do tempo, representado na figura acima, a área sombreada (em amarelo) é numericamente igual ao módulo do impulso.
área=(altura).(base)
|I|=F .(∆t)
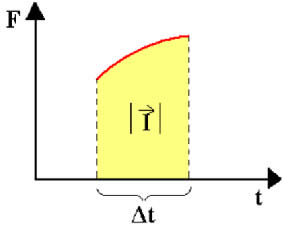
Usando em seguida o mesmo tipo de argumentação do caso do trabalho de uma força, podemos concluir que, no caso da figura abaixo, em que apenas o módulo de  varia, a área também nos dá o módulo do impulso da força no intervalo de tempo Δt. Porém, vale a pena repetir: essa propriedade só vale se a direção da força for constante.
varia, a área também nos dá o módulo do impulso da força no intervalo de tempo Δt. Porém, vale a pena repetir: essa propriedade só vale se a direção da força for constante.
Equação geral do Impulso
O impulso de uma força qualquer, num intervalo de tempo Δt, é igual à variação da quantidade de movimento produzida por essa força no intervalo de tempo Δt. Portanto, temos: