No estudo das características dos espelhos esféricos vimos que é possível construir graficamente a imagem conjugada por um dado espelho esférico. Nesse momento, vamos determinar algebricamente a imagem formada em um espelho esférico côncavo, sua posição e altura. Para isso, basta conhecer a posição e a altura do objeto.
Um sistema de coordenadas conveniente é o chamado referencial de Gauss, um referencial cartesiano que se faz coincidir com o esquema de espelho, de forma que:
► O eixo das abscissas coincide com o eixo principal do espelho
► O eixo das ordenadas coincide com o espelho
► A origem coincide com o vértice do espelho
O eixo das abscissas é orientado em sentido contrário ao da luz incidente, de modo que os elementos reais tenham abscissas positivas, e os elementos virtuais tenham abscissas negativas. Na figura abaixo, para um espelho côncavo de Gauss (cuja parte refletora é a interna, indicando por p a abscissa do objeto e por p’ a abscissa da imagem), temos:
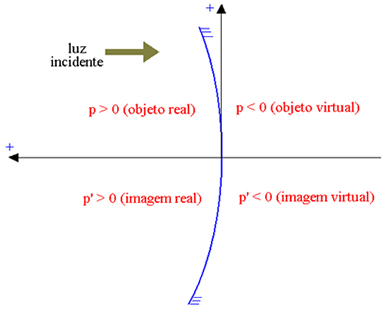
Objeto real: p > 0; objeto virtual: p < 0; imagem real: p’ > 0; imagem virtual: p’ < 0.
Com as convenções adotadas, o foco principal tem abscissa positiva se o espelho é côncavo – foco real; e negativa para os espelhos convexos – foco virtual.
♦ Espelho côncavo: f > 0
♦ Espelho convexo: f < 0
A equação que relaciona as abscissas do objeto (p), da imagem (p’) e do foco (f) é chamada de equação de Gauss ou equação dos pontos conjugados:
Para a demonstração da equação de Gauss, vamos considerar um objeto 
e sua correspondente imagem .jpg){kind=small}
conjugada por um espelho esférico côncavo, conforme a figura abaixo.
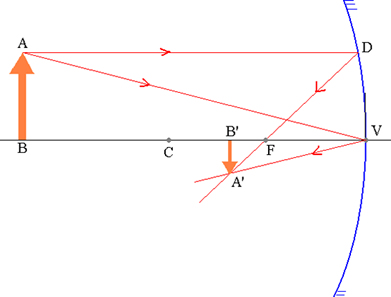
Objeto AB e sua correspondente imagem A’B’ em um espelho esférico.
Os triângulos ABV e A’B’V são semelhantes:
mas VB’ = p’ e VB = p. Portanto,
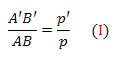
Os triângulos FDV e FA’B’ também são semelhantes. Mas DV = AB, FB’ = p’- f e FV = f. Logo,
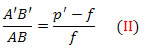
Das equações (I) e (II),
Dividindo ambos os membros por pp’f, temos:
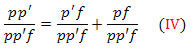
Portanto,
