É comum olharmos para um objeto que se encontra dentro da água e termos a impressão de que ele está mais perto da superfície. Outra observação que fazemos é em relação à profundidade de uma piscina cheia, nesse caso, quando ela está totalmente cheia, temos a impressão de que ela é mais rasa do que realmente parece. Nessa situação o que vemos é a imagem de um objeto, determinada pela luz que se refratou ao atravessar a superfície de separação entre o ar e a água.
Em física definimos um dioptro plano como sendo o conjunto constituído por dois meios transparentes (ar-água) separados por uma superfície plana. O exemplo mais comum de dioptro plano é a superfície de uma piscina.
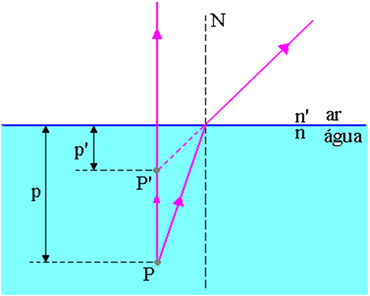
Na figura acima temos que p é a distância do ponto objeto P até a superfície ar-água, p’ é a distância do ponto imagem P’ à superfície ar-água, n é o índice de refração do meio de incidência e n’ é o índice de refração do meio de emergência da luz, isto é, é o índice de refração do meio onde se encontra o observador.
A equação de Gauss para os dioptros planos é dada através da seguinte relação matemática:
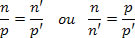
Essa relação pode ser determinada aplicando a Lei de Snell-Descartes à situação da figura abaixo.

Como os ângulos de incidência (i) e reflexão (r) são muito pequenos podemos considerar que:
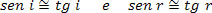
Portanto,
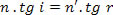
Mas como,
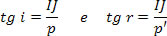
temos:
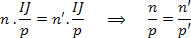
Na equação temos que:
- n é o índice de refração do meio em que se encontra o objeto
- n’ é o índice de refração do meio em que se encontra o observador
- p é a distância do ponto objeto e a superfície do dioptro plano
- p’ é a distância do ponto imagem e a superfície do dioptro plano


