Algumas pessoas fazem uso de um acessório que permite a correção visual. Elas usam óculos para corrigir uma deficiência visual ou apenas para leitura. Como sabemos que a maioria das “coisas” que nos rodeiam funciona se baseando nas leis da física, os óculos não ficam de fora.
Até mesmo os fabricantes desses acessórios devem conhecer um pouco de física. Portanto, podemos calcular a distância focal f de uma lente se conhecermos o índice de refração n do material e os raios de curvatura R1 e R2 das superfícies. Lembre-se que a distância focal de uma lente também depende do índice de refração do meio em que ela está imersa (nmeio).
Para o cálculo da distância focal f de uma lente, os fabricantes utilizam a seguinte expressão:
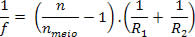
Na equação acima, temos que se a superfície for convexa, o sinal do raio de curvatura R será positivo; e se a superfície for côncava, o sinal do raio de curvatura R será negativo. A concavidade da superfície é determinada no sentido de fora para dentro da lente. Na figura abaixo, ambas as superfícies são convexas, portanto os valores de R1 e R2 são positivos.
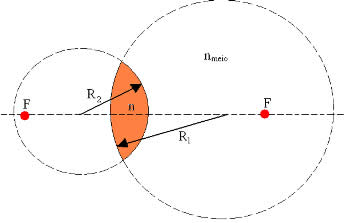
Lentes convexas
Quando a lente estiver no ar, nlente = 1, uma lente biconvexa será convergente, pois a distância f é positiva. Entretanto, se colocarmos essa lente em um líquido cujo índice de refração seja maior do que o da lente (nmeio > n), sua distância focal será negativa, indicando que a lente passa a ser divergente nesse meio. Da mesma forma, uma lente divergente imersa nesse líquido se tornará convergente.


